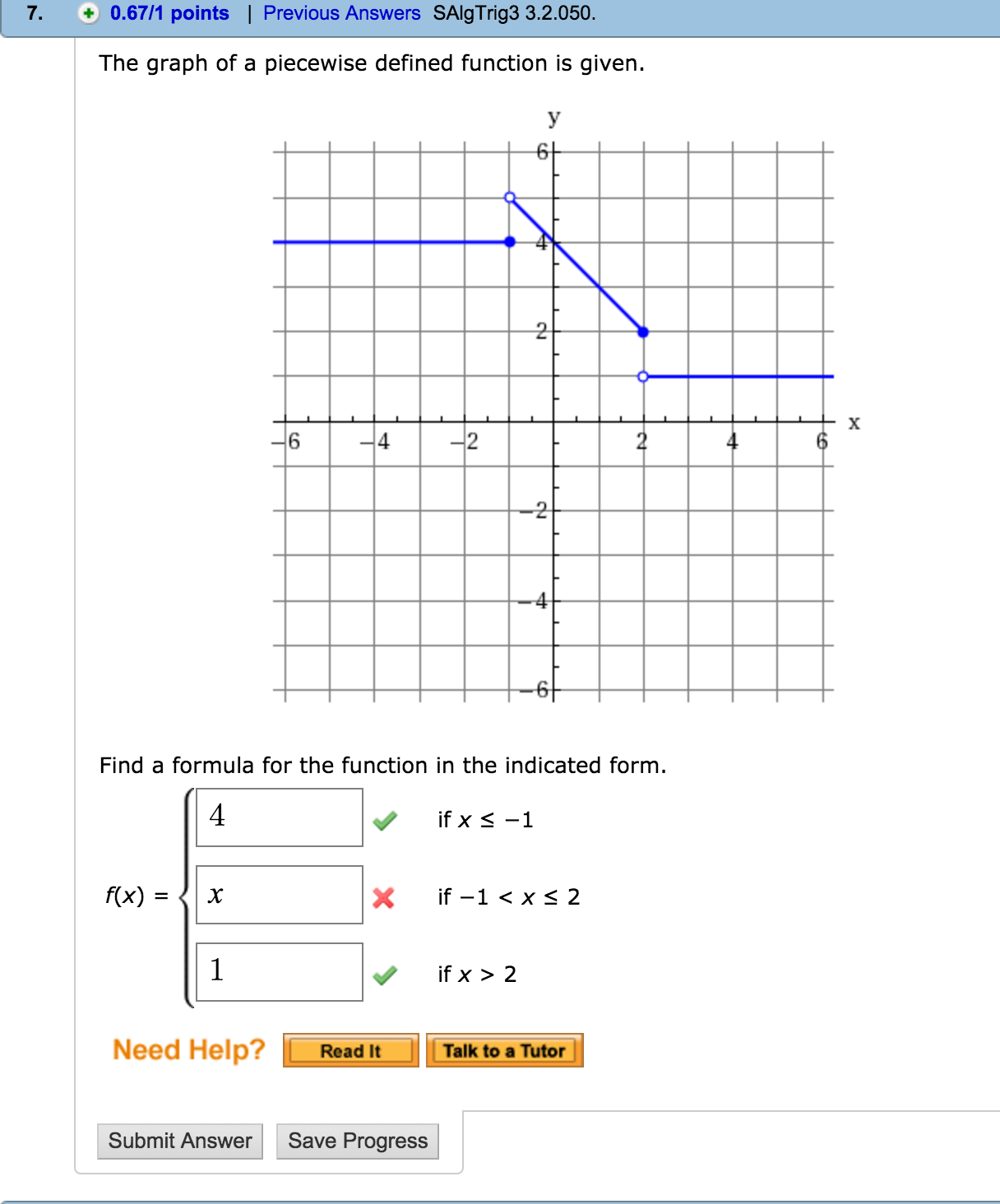
How do you graph the greatest integer function on a TI Nspire?
Enter the function piece in the numerator and enter the corresponding interval in the denominator.Press to insert the n/d fraction template in the Y= editor.Here are the steps to graph a piecewise function in your calculator: Repeat Steps 1 through 3 to graph additional inequalities.Īlso Know, how do you graph piecewise functions on a calculator?.Type a number to choose your inequality, and press to view its graph.Press until the equals sign is deleted.Press to open the entry line and position the cursor to the right of the first available function.
#GRAPHING PIECEWISE FUNCTIONS HOW TO#
Type x for the argument and press to complete the graph.įurthermore, how do you graph inequalities on a TI Nspire CX? How to Graph Inequalities on the TI-Nspire. Press to jump to the items beginning with I, scroll down, highlight int, and press to paste this command to the Graphs entry line. Position the cursor next to the first available function line. Graph a Step Function in TI-Nspire Graphs Application People also ask, how do you graph a step function on a TI Nspire CX? Press to graph the piecewise function. Press or use the Touchpad keys to navigate the template. Edit the expression and condition for each piece. Type the number of function pieces when prompted. So to find the range of a piecewise function, graph it first. The range is the set of all y-values that its graph covers. The domain of a piecewise function is the union of all intervals that are given in its definition. How to Find Domain and Range of a Piecewise Function? Its graph has more than one part and yet it is possible to graph it without lifting the pencil. What is a Piecewise Continuous Function?Ī piecewise continuous function is a function that is piecewise and continuous. For example, the absolute value function, step function (floor function or greatest integer function), ceiling function, etc are examples of piecewise linear functions.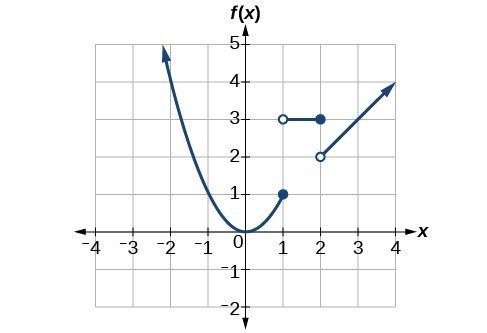 
Give an Example of a Piecewise Linear Function.Ī piecewise linear function is a piecewise function in which all pieces correspond to straight lines. Substitute the given input in the function from the last step.Just see which of the given intervals that input lies in.To solve the value of a piecewise function at a specific input: If the left/right endpoint is ∞ or -∞ then extend the curve on that side accordingly.Plot all the points (put open dots for the x-values that are excluded) and join them by curves.Substitute every x value in the corresponding expression of f(x) that gives value in the y-column.Include endpoints (in the column of x) of each interval in the respective table along with several other random numbers from the interval.Make a table (with two columns x and y) for each definition of the function in the respective intervals.Here is an example to understand these steps.Įxample: Graph the piecewise defined function \(f(x)=\left\\right.\). Now, just plot all the points from the table (taking care of the open dots) in a graph sheet and join them by curves.Substitute each x value from every table in the corresponding definition of the function to get the respective y values.Take 3 or more numbers for x if the piece is NOT a straight line. If the piece is a straight line, then 2 values for x are sufficient.
In each table, take more numbers (random numbers) in the column of x that lie in the corresponding interval to get the perfect shape of the graph. If the endpoint is excluded from the interval then note that we get an open dot corresponding to that point in the graph. Include the endpoints of the interval without fail. Make a table with two columns labeled x and y corresponding to each interval. Write the intervals that are shown in the definition of the function along with their definitions. For example, f(x) = ax + b represents a linear function (which gives a line), f(x) = ax 2 + bx + c represents a quadratic function (which gives a parabola), etc, so that we will have an idea of what shape the piece of the function would result in. First, understand what does each definition of the function represents. Here are the steps to graph a piecewise function. We already know that the graph of a piecewise function has multiple pieces where each piece corresponds to its definition over an interval.
0 kommentar(er)
